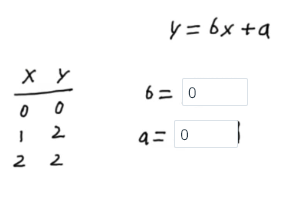35. Final Exam
Part 1
Note: Very trivial questions are left out, and only those I find difficult or might be helpful to note down with explanation or just for calculation purposes are tackled here.
Question 4¶

%load_ext tikzmagic
from graphviz import Digraph
from helpers import update_samecoin_graph
def draw_samecoin_graph(g, n_flips=2, highlight_nodes=[], color='yellow'):
g.attr(rankdir='LR', ranksep='0.5')
g.attr('node', shape='circle', fontsize='10')
g.attr('edge', fontsize='10')
g.node('Root','R')
g.node('H0','H') # Fair coin
g.node('T0','T') # loaded coin
# print('noding')
i_outcome = 1
for each_flip in range(1,n_flips):
n_outcomes = 2**each_flip
for each_outcome in range(0, n_outcomes):
new_H = 'H{}'.format(i_outcome)
new_T = 'T{}'.format(i_outcome)
g.node(new_H, 'H')
g.node(new_T, 'T')
i_outcome += 1
# choose F or L
g.edge('Root','H0',label='0.7')
g.edge('Root','T0',label='0.3')
# flip 1 of H/T (F or L is not considered a flip)
g.edge('H0','H1',label='0.5')
g.edge('H0','T1',label='0.5')
g.edge('T0','H2',label='0.5')
g.edge('T0','T2',label='0.5')
for each_node in highlight_nodes:
#print(each_node)
g.node(each_node,style='filled',fillcolor=color)
return g
g = Digraph()
g = draw_samecoin_graph(g) # hardcoded for this problem now
# Root - Choosing between Fair or Lodged Coin
g = update_samecoin_graph(g, highlight_nodes=['Root'],color='#33EA4C:#A2E9FF')
g = update_samecoin_graph(g, highlight_nodes=['H0','T1'],color='#A2E9FF')
g
Answer: $P(H_l)p(T_l) = (0.7)(0.5) = 0.35$
g = Digraph()
g = draw_samecoin_graph(g) # hardcoded for this problem now
# Root - Choosing between Fair or Lodged Coin
g = update_samecoin_graph(g, highlight_nodes=['Root'],color='#33EA4C:#A2E9FF')
g = update_samecoin_graph(g, highlight_nodes=['H0','T1'],color='#A2E9FF')
g = update_samecoin_graph(g, highlight_nodes=['H0','H1'],color='#A2E9FF')
g = update_samecoin_graph(g, highlight_nodes=['T0','H2'],color='#A2E9FF')
g
$$ P( \text{H in any flip} ) = \dfrac{(0.7)(0.5) + (0.7)(0.5) + (0.3)(0.5)}{(0.7)(0.5) + (0.7)(0.5) + (0.3)(0.5) + (0.3)(0.5)} = 0.85 $$
0.7*0.5+0.7*0.5+0.3*0.5
Question 6¶
def draw_samecoin_graph(g, n_flips=2, highlight_nodes=[], color='yellow'):
g.attr(ranksep='0.5')
g.attr('node', shape='circle', fontsize='10')
g.attr('edge', fontsize='10')
g.node('Root','R')
g.node('H0','H') # Fair coin
g.node('T0','T') # loaded coin
# print('noding')
i_outcome = 1
for each_flip in range(1,n_flips):
n_outcomes = 2**each_flip
for each_outcome in range(0, n_outcomes):
new_1 = '1{}'.format(i_outcome)
new_2 = '2{}'.format(i_outcome)
new_3 = '3{}'.format(i_outcome)
new_4 = '4{}'.format(i_outcome)
new_5 = '5{}'.format(i_outcome)
new_6 = '6{}'.format(i_outcome)
g.node(new_1, '1')
g.node(new_2, '2')
g.node(new_3, '3')
g.node(new_4, '4')
g.node(new_5, '5')
g.node(new_6, '6')
i_outcome += 1
# choose F or L
g.edge('Root','H0',label='0.5')
g.edge('Root','T0',label='0.5')
g.edge('H0','11',label='0.166')
g.edge('H0','21',label='0.166')
g.edge('H0','31',label='0.166')
g.edge('H0','41',label='0.166')
g.edge('H0','51',label='0.166')
g.edge('H0','61',label='0.166')
g.edge('T0','12',label='0.125')
g.edge('T0','22',label='0.125')
g.edge('T0','32',label='0.125')
g.edge('T0','42',label='0.125')
g.edge('T0','52',label='0.125')
g.edge('T0','62',label='0.125')
g.edge('T0','7',label='0.125')
g.edge('T0','8',label='0.125')
for each_node in highlight_nodes:
#print(each_node)
g.node(each_node,style='filled',fillcolor=color)
return g
g = Digraph()
g = draw_samecoin_graph(g) # hardcoded for this problem now
# Root - Choosing between Fair or Lodged Coin
g = update_samecoin_graph(g, highlight_nodes=['Root'],color='#33EA4C:#A2E9FF')
g = update_samecoin_graph(g, highlight_nodes=['H0','61'],color='#A2E9FF')
g = update_samecoin_graph(g, highlight_nodes=['T0','62'],color='#A2E9FF')
g
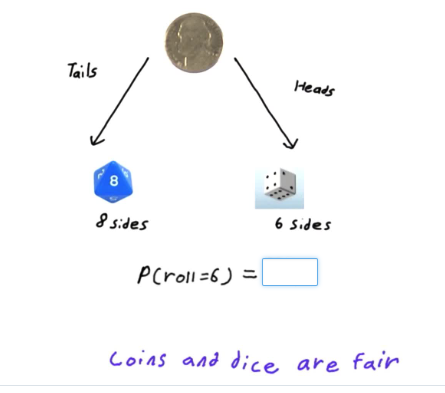
As can be seen above, there are 2 cases possible for getting 6. So
$$ P( \text{getting 6} ) = (0.5)(0.166) + (0.5)(0.125) = 0.145 $$
(0.5)*(0.166) + (0.5)*(0.125)
Question 7¶
In same case above, what is $P( \text{heads} | 6)$? As we just saw, there are totally 2 cases of getting 6, which has probability of 0.145. Out of which, one case has heads. So
$$ P(\text{heads} | 6) = \dfrac{(0.5)(0.166)}{0.145} = 0.572 $$
0.5*0.166/0.145
Question 8¶

Out of $n=7$ days, we want to know the probability of $r=2$ days having rain. Comparing an analogy to coin flip, the no of flips is to no of days, and each outcome is whether we get rain or not. Thus its a binomial distribution.
$$ P(\text{rain for 2 days}) = \binom{n}{r}p^r(1-p)^{n-r} = \binom{7}{2}(0.2)^2(1-0.2)^{7-2} = 0.275 $$
21*((0.2)**2)*((0.8)**5)
Question 9¶
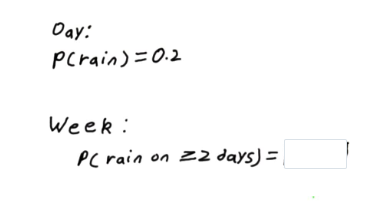
Answer is just add individual probabilities for different r as below. $$ P(X \geq x) = P(X \geq 2) = P(X=2) + P(X=3) + P(X=4) + P(X=5) + P(X=6) + P(X=7) = 0.423 $$
from math import sqrt
n, p, q = 7 ,0.2, 1 - 0.2
r = 2
from scipy.stats import binom
tp = 0
for i in range(2,8):
tp += binom.pmf(i, n, p)
tp
Part 2
Question 10¶
What is the z score?
$$ \mu = 100, \ \ \sigma = 15, \ \ X = 130 \\ Z = \dfrac{X - \mu}{\sigma} = 2 $$
$$ E(X - Y) = E(X) - E(Y) = 10 - 5 = 5 \\ Var(X-Y) = Var(X) + Var(Y) = \sigma_X^2 + \sigma_Y^2 = 1^2 + (0.5)^2 \\ \sigma_{X-Y} = \sqrt{Var(X-Y)} = 1.12 $$
from math import sqrt
s_r = sqrt(1**2 + 0.5**2)
s_r
Question 12¶

Ans:
$$ E(aX) = aE(X) = 2.54(70) = 177.8 \\ Var(aX) = a^2Var(X) = (2.54)^2(25) = 161.29 \\ $$
m = 2.54*70
v = ((2.54)**2)*25
m,v
Question 13¶
Note carefully. They are asking CI for the probability.

For a single Bernoulli trial, we could thus have an estimate as below from the 10000 trials.
$$ \hat{p} = \dfrac{4950}{10000} = 0.4950 \\ \overline{x} = \hat{p} = 0.4950 \\ s = \sqrt{pq} = \sqrt{(0.495)(1-0.495)} = 0.4999 $$
p = 4950/10000
m = p
s = sqrt( 0.4950*(1-0.495) )
s
Calculating Critical Value $z_{\frac{\alpha}{2}}$¶
If confidence level is 90\%, then significance level $\alpha$ is 10\%, thus respective Z value would be 1.645
def get_z(cl):
#NOTE:returns right tailed area as that is mostly used in CI
from scipy import stats
alpha = round((1 - cl)/2,3)
return (-1)*round(stats.norm.ppf(alpha),3) # right tailing..
cl = 0.90
print(get_z(cl))
Calculating CI¶
Since we are repeating for $n=10000$ trials, we expect a sampling distribution as below. Calculating CI for the same,
$$\begin{aligned} CI &= \overline{x} \pm z_{\frac{\alpha}{2}}\dfrac{s}{\sqrt{n}} \\ &= 0.4950 \pm 1.645\dfrac{0.4999}{\sqrt{10000}} \\ &= 0.4950 \pm 1.645(0.004999) \\ &= (0.4867, 0.5032) \end{aligned}$$
0.4950 - 1.645*0.004999, 0.4950 + 1.645*0.004999
%matplotlib inline
import matplotlib.pyplot as plt
# from normalviz import draw_normal
import numpy as np
import matplotlib.mlab as mlab
import math
def draw_normal(ax, mu, sigma, cond=''):
"""
cond: to shade the area meeting the condition
"""
xstart = mu - 4*sigma
xend = mu + 4*sigma
x = np.linspace(xstart, xend, 100)
y = mlab.normpdf(x, mu, sigma)
ax.plot(x,y, color='black')
# shade area satisfying the condition
w = x[eval(cond)] if cond != '' else x
w_shade = mlab.normpdf(w, mu, sigma)
ax.fill_between(w, 0, w_shade)
# set x axis in multiples of sigma
x_ticks = []
for step in range(-4,5): # 4 sigma on right, 4 on left, mu on middle
x_tick = round(mu + (step)*sigma,2)
x_ticks.append(x_tick)
ax.xaxis.set_ticks(x_ticks)
ax.grid(True, linestyle='--',alpha=0.5)
ax.set_ylim(ymin=0)
mu = 0.4950
sigma = 0.004999
# plot
fig, ax = plt.subplots(1,1, figsize=(7,4))
draw_normal(ax, mu, sigma, 'x<0.4867')
draw_normal(ax, mu, sigma, 'x>0.5032')
ax.set_xlabel('No of flips')
ax.set_ylabel('Probability that they are heads')
plt.show()
Question 14¶

x = [0.79,0.70,0.73,0.66,0.65,0.70,0.74,0.81,0.71,0.70]
n = len(x)
xb = sum(x)/n
v = sum([ (i - xb)**2 for i in x ] )/n
s =sqrt(v)
xb, s
se = 1.96*(s/sqrt(n))
xb - se, xb + se
x = [0,1,2]
y = [0,2,2]
# means
n = len(x) # also could use len(Y) as its pairs
x_b, y_b = sum(x)/n, sum(y)/n
b_1 = sum([(i[0] - x_b)*(i[1] - y_b) for i in zip(x,y)])/ sum([(i - x_b)**2 for i in x])
b_0 = y_b - b_1*x_b
b_0, b_1